正規分布(normal distribution)の確率密度関数は下記の式で表される。
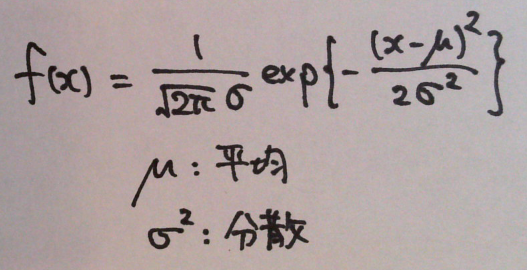
f(x) は確率密度関数なので、全区間で積分すると1になる。正規分布が 平均 μ, 標準偏差 σ に従うことを省略して、
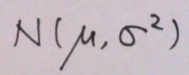
と表記することもある。ちなみにExcelで “=NORM.DIST(x, μ, σ, FALSE)” とすれば、正規分布のグラフを描くことができる。
平均 μ を変えると、正規分布はx方向にスライド。
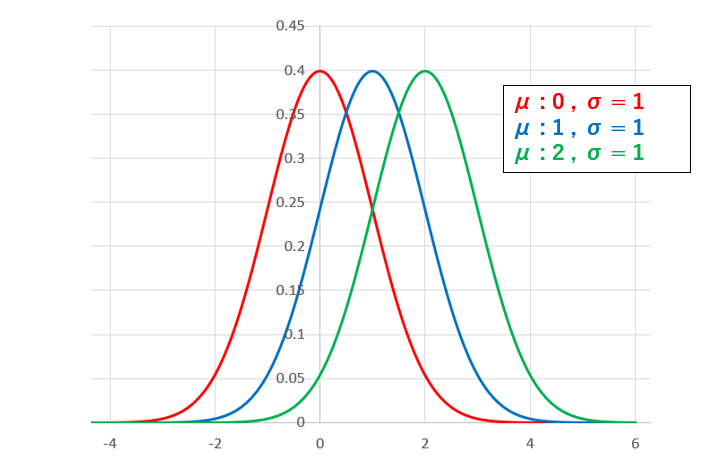
標準偏差 σ が大きいほど、分布は広がっていく。
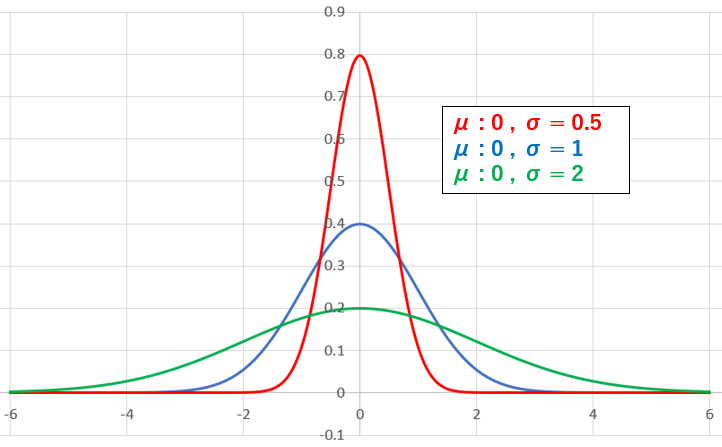
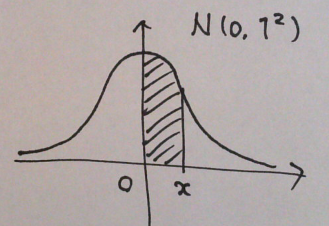
特に、平均 : 0, 分散 : 1 であるときは、標準正規分布と呼ばれる。
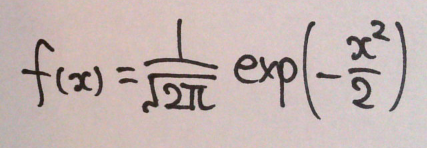
■標準正規分布表
標準正規分布において、0~xの区間(斜線部分の面積)が全体の何%にあたるのかを確認できる標準正規分布表というものがある。
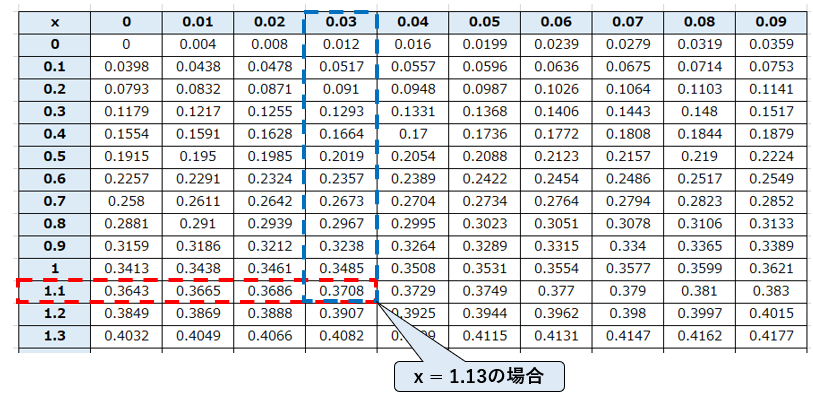
例えば、x = 1.13のとき、つまり 0~1.13の区間が全体の何%にあたるのかを求めたい場合。表の”1.1″行と”0.03″列の交差するセルの数値を参照すればよい。x = 1.13 の場合は0.3708なので、斜線部分の面積が全体の37.08%であることがわかる。
どんな正規分布であっても、標準化することができるので、標準正規分布表の値を利用することができる。
■正規分布と σ 区間に含まれる確率
正規分布であれば(標準正規分布でなくても)
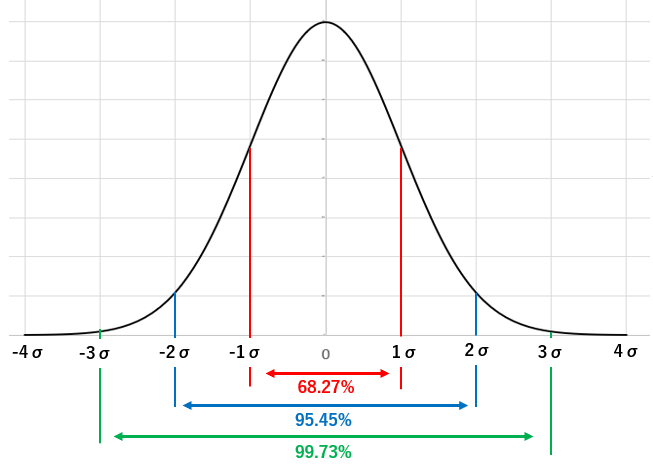
・μ-σ ~ μ+σ の区間に含まれる確率は68.27%
・μ-2σ ~ μ+2σ の区間に含まれる確率は95.45%
・μ-3σ ~ μ+3σ の区間に含まれる確率は99.73%
・μ-4σ ~ μ+4σ の区間に含まれる確率は99.994%
・μ-5σ ~ μ+5σ の区間に含まれる確率は99.99994%
・μ-6σ ~ μ+6σ の区間に含まれる確率は99.9999998%
となる。σ~3σ区間については、簡略表現でまとめて “68-95-99.7則” と呼ばれてたりする。
●誤差関数 erf
正規分布に関連して、誤差関数 erf (error function)というものがある。erf の定義は下記の通り。※係数とexp( )の中身が、標準正規分布と異なるので注意。
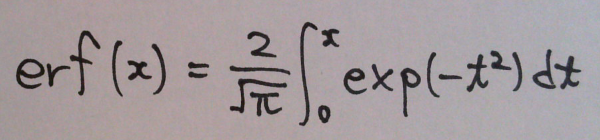
正規分布の μ-xσ ~ μ+xσ 区間の面積が全体の何%にあたるのかは
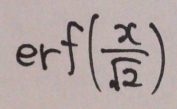
で求められる。erf で x/√2とするのは、下記の通り、標準正規分布で考えたときに、積分範囲を 0~x に合わせるため。
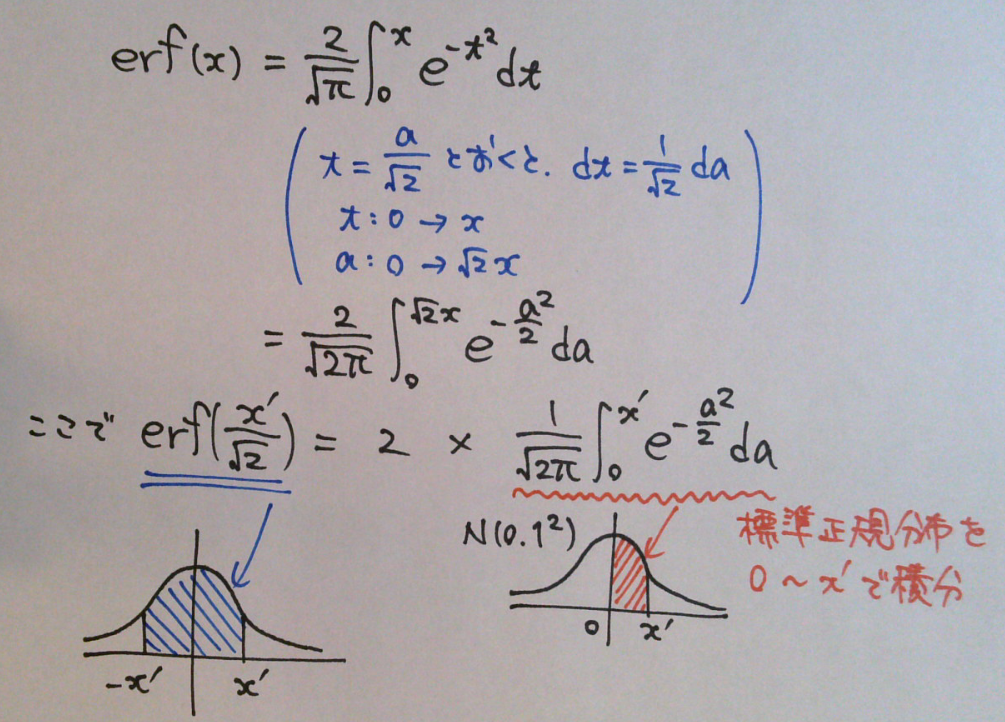
ちなみに、Excelで “=ERF(3/SQRT(2))” とすれば、μ-3σ ~ μ+3σ の区間に入る確率である0.9973…(99.73%) が値として返ってくる。
●相補誤差関数 erfc
逆に μ-xσ ~ μ+xσ の”区間外”に含まれる確率は
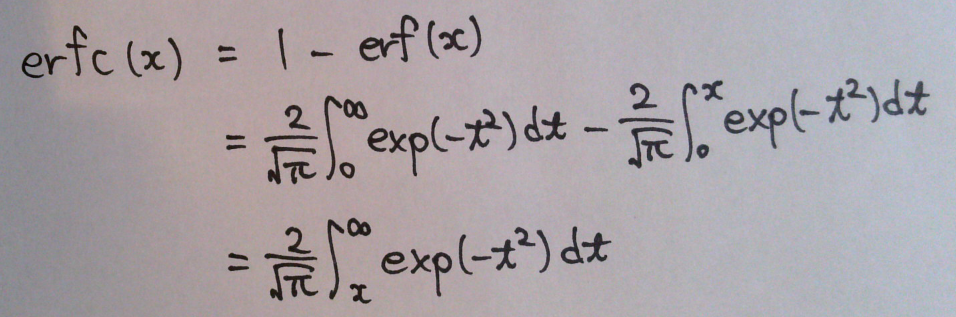
で求められ、erfc は相補誤差関数(complementary error function)と呼ばれる。余誤差関数とも呼ばれたりする。
例えば、Excelで “=ERFC(3/SQRT(2))” とすれば、μ-3σ ~ μ+3σ の区間外に含まれる確率である0.002699…(0.27%) が値として返ってくる。