※なんとなくの理解度で書いてるメモ書きなので、厳密な数学を知りたい方は教科書をご参照ください…
■まずはフーリエ級数の例 (イメージを掴む)
ある関数 f(θ) をサイン、コサインの足し算で表せるというもの。
例えば、方形波は sin の奇数倍の足し合わせで表現できる。

方形波をフーリエ級数展開すると
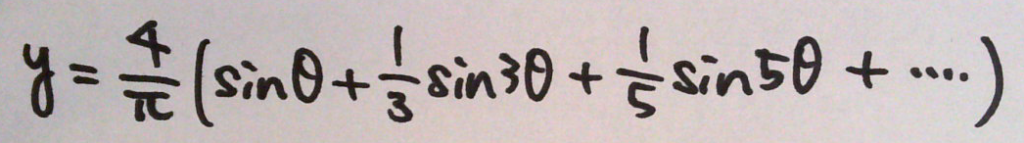
方形波のフーリエ級数をExcelで計算してみた。図2のフーリエ級数において、計算する項数を増やすほど、方形波に近づいていくことがわかる。
↓第2項のsin3θの項まで計算したとき

↓第4項のsin7θの項まで計算したとき

↓第8項のsin15θの項まで計算したとき
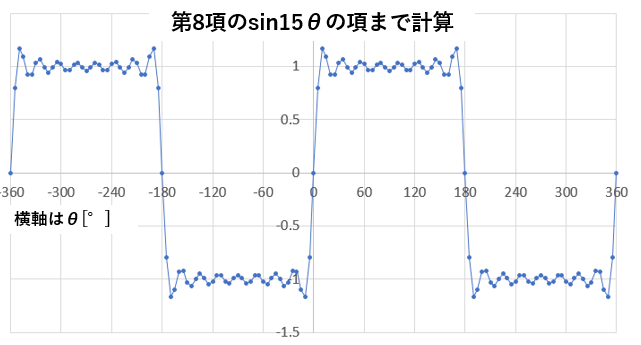
上記のように、複雑な波形であっても、sinやcosの足し合わせで表現できるのがフーリエ級数であり、電気工学の分野ではとても重要になってくる。(別記事で触れる予定)
では、フーリエ級数をこれから導出していく。
■奇関数・偶関数
フーリエ級数を導く上で、奇関数と偶関数の性質を利用するので説明。
●奇関数
原点を中心にして点対称になる関数 f(x) = -f(-x)
例えば、下記の通り。
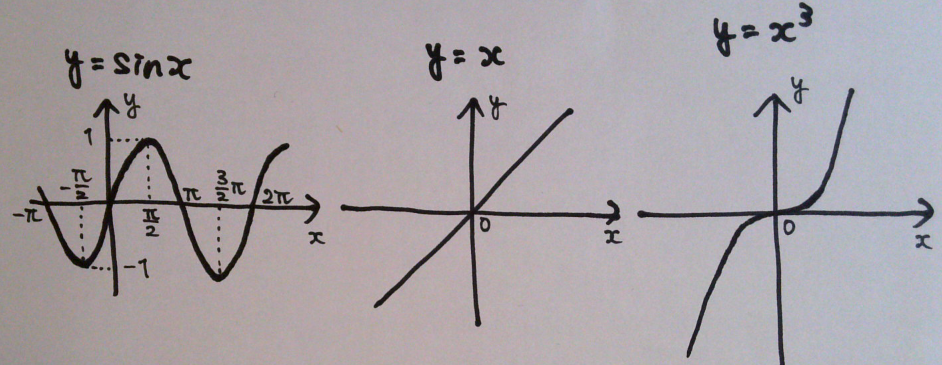
奇関数は -a ~ +a の区間で積分すると0になる。
プラスの領域とマイナスの領域が同じ面積だから。

●偶関数
y軸に対して対称の関係になる関数 f(x) = f(-x)
例えば、下記の通り。
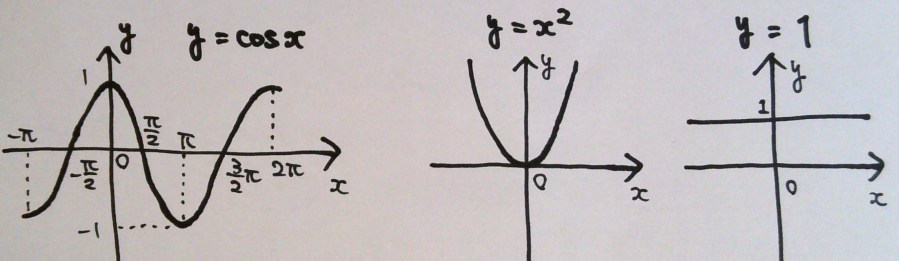
偶関数は -a ~ +a の区間で積分する場合、
0 ~ +a の区間で積分したものを2倍した値と同じになる。
y軸の左側も、右側も、(符号も含めて)同じ面積となっているため。
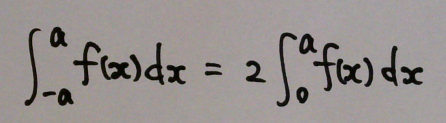
●奇関数と偶関数の積
奇関数と偶関数は掛け算すると、下記の通り。
[1] 奇関数 × 奇関数 = 偶関数
[2] 奇関数 × 偶関数 = 奇関数
[3] 偶関数 × 偶関数 = 偶関数
例えば、
奇関数 : y = x
偶関数 : y = 1
として、それぞれの掛け算を考えてみると、イメージしやすい。
■三角関数の直交性
フーリエ級数を導く上で、三角関数の直交性を利用するので説明。”関数を掛け算して積分すると0になる” = “それぞれの関数は直交している” と表現する。
●sin × sin の場合
下図の sin × sin の 式について考えてみる。m, nは整数とする。

[1] m ≠ n の場合
積分は0になる。

[2] m = n の場合
積分はπになる。
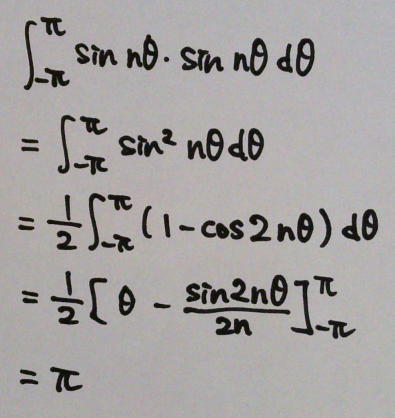
上記の結果をまとめると、下式のようになる。
右辺の記号はクロネッカーのデルタで、m=nのときは1、m≠nのときは0
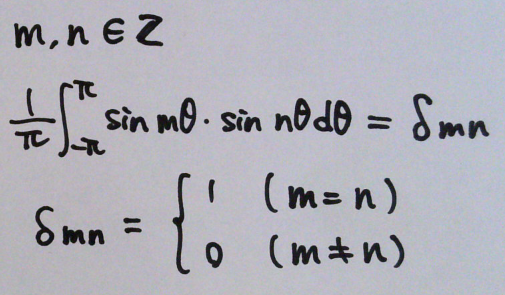
●cos × cos の場合
sin × sin と同様に考えればOK。
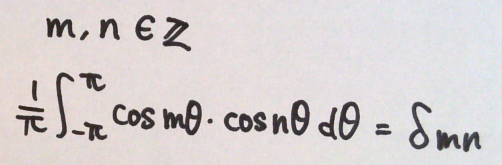
●sin × cos の場合
sin は奇関数、cos は偶関数であり、その積は奇関数。
奇関数を -a ~ +a の範囲で積分すると0になるので、下式の通り。

上の例だと、sin(mθ) と cos(nθ) は直交していることになる。
■フーリエ級数
ある関数 f(θ) をサインとコサインの足し算で表せたとすると、一般式は下記のようになるはず。
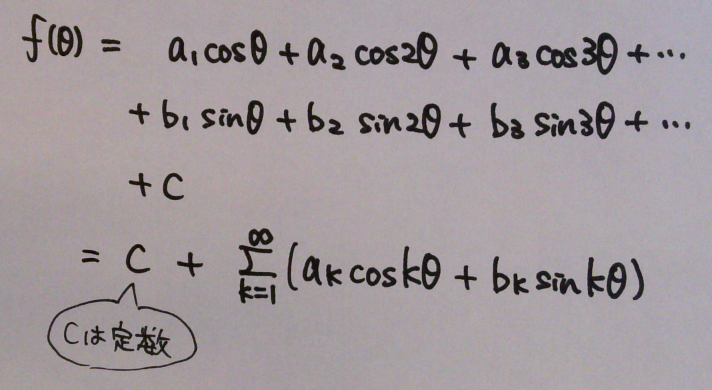
ここで、定数Cと係数a, bがわかれば、関数 f(θ) をサインとコサインの足し算で表せるということになる。
●係数 a を求める
a1 を求める。両辺に cosθ を掛けて、-π~+π まで積分。

この調子で、
a2 を求めるときは、 両辺に cos2θ を掛けて、-π~+π まで積分。
a3 を求めるときは、 両辺に cos3θ を掛けて、-π~+π まで積分。
と考えていけばOK。まとめると、
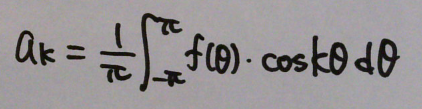
●係数 b を求める
考え方は係数 a を求めるときと同じで、
b1 を求めるときは、 両辺に sinθ を掛けて、-π~+π まで積分。
b2 を求めるときは、 両辺に sin2θ を掛けて、-π~+π まで積分。
と考えていけばOK。まとめると、
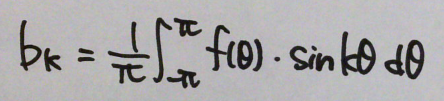
●定数 C を求める
両辺を -π~+π まで積分。すると、cosおよびsinの積分は0になるので、定数Cの項だけ残る。

定数Cは求まったが、Cは係数 a の形式に合わせて書くことができる。図18の係数 a の数式で、k=0の場合を考えると、
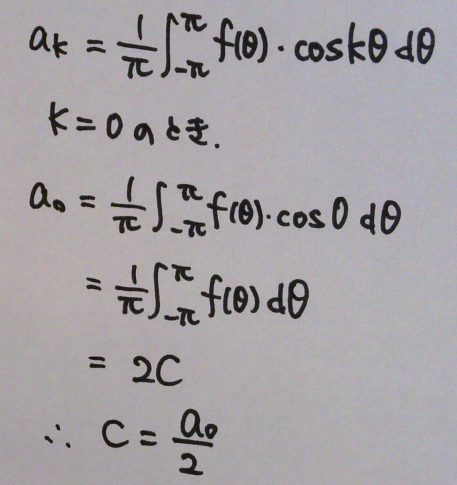
●フーリエ級数
ここまでの内容をまとめよう。ある関数 f(θ) はサイン、コサインの足し合わせで表すことができる。これを f(θ) のフーリエ級数 または フーリエ級数展開という。
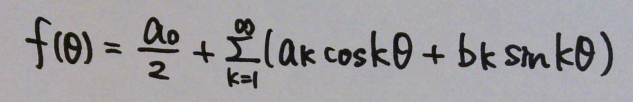
このとき f(θ) から求められる係数 a, b をフーリエ係数という。

別記事で、いくつかの関数のフーリエ級数展開を、実際にやってみることにする。